- Basic Poker Statistics Definition
- Basic Poker Statistics Games
- Basic Poker Statistics For Dummies
- Basic Poker Statistics Cheat
Introduction to the Mathematics of Poker
Learn the Mathematics of Poker, Basic Statistics, and Probability PokerVIP Coaching. 7,775 Views. 2 Comments. on 28/8/15 The mathematics of poker don't need to be complicated. The main underpinning of poker is math. Psychology has a part to play, but a solid understanding of probability will serve you well at the poker tables.
Let me get you a little bit into the math of poker. First of all, let’s consider its importance on a hand-to-hand basis. First of all, when you’re dealt a hand in poker, and it’s your turn to act, depending on the action that you got from the other players who acted before you, you have to make the decision either to raise, call or fold.
First of all, you consider your hand. Is it a strong hand that I could get all my money in pre-flop with and be profitable? Or do I have a drawing hand, like a suited connector? And what amount of big blinds can I call at most in this spot to be able to
play my hand profitably on the river? Can I re-raise as a bluff and will this bring me profit in the long run?
If all the answers here are no, no and no then you’re going to fold. But are you sure you calculated it correctly? We’ll get into depth on these matters in this article.
Also, let’s say you hold a strong top pair and you’ve got to the river with it, and your opponent over-bet shoves. Do we have the right odds to call here? What is he representing here? And can we put him on a range? And after that can we call profitably? These questions will be answered also.
Pot Odds
I always go for percentages everywhere in poker, because I find it a lot easier to understand and also apply. The first thing I learned when I was starting out with poker, was pot odds, and I think they should be the foundation to every poker player’s knowledge.
To explain this as simple as do re mi, for you to be profitable, the breakeven equity that you need to make a call when you get bet into, is the amount that you have to put into the pot divided by the total pot size (including your bet – so the amount that you’re winning when you have the stronger holding).
Let’s first take an example:
You are playing poker against Phil Ivey, and he bets into you on the river. You’re currently holding AJ, and the board is A2742. Some guy told you that he could either have AT, AJ, AQ or AK, and you’re facing a 2/3 pot bet.
Let’s face it, you’re behind. But what is the amount of hands that beats you relative to the size of the bet you have to call? Good question.
So you beat AT and get beat by AQ and AK, and split with AJ, which we shall discount because it’s 0 EV.
Obviously, the same number of combinations exist for AT, AQ and AK, so we win 1 time out of three!
Our estimated equity is 33%, but are the pot odds low enough? If they are, it’s a sure call!
This is how you calculate:
You need to call 2/3 into a pot that will contain your 2/3 bet, the pot size which is 3/3 and the opponent’s bet which is also 2/3. That means that you have to call 2/3 to win a pot of 7/3, so your breakeven equity will be:
Basic Poker Statistics Definition
(2/3)/(7/3)*100(to display in percentage) = (2/7)*100 = 28%.
We know from the logic above that we have 33% equity, so we have greater equity than the pot odds, so even though we’re behind, we can still call here profitably!
You have 1 dollar and you hate bluffing, but someone offers you the chance to crack his pocket AA’s with 72o and win 100 dollars if you do it. Assuming this is a legit deal, you only need to put in 1 dollar to win 100 so this is
(1/100)*100=1% breakeven frequency.
Last time I checked Equilab, 72o has around 12% chance to crack aces, so it’s a sure call. I would take this deal every time I get the occasion. Here are some default pot odds that you should know by heart, because they will prove very useful when thinking about calling:
- 1/3 Pot – 20%
- 1/2 Pot – 25%
- 2/3 Pot – 28%
- 3/4 Pot – 30%
- 4/5 Pot – 31%
- Full Pot – 33%
- 1.5x Pot – 37%
- 2x Pot – 40%
Fold equity
If you’re the one who’s betting, there’s always a combination of your hand’s equity and your total fold equity involved. Let’s say you’re bluffing the river this time, and you’re wondering how to determine the amount of times he has to fold to make your bet profitable, look no further!
Let’s say that we’re betting with a hand that, if we get called, we can never win, like a busted flush draw on the river. If we think that the opponent will fold enough times, we can make this bet.
The formula is: Breakeven Fold Equity = (your bet) divided by (the sum of your bet and the pot size).
Thinking about this, it becomes quite logical that if you bet full pot, you need him to fold 50% of the time, because
1/(1+1) = 1/2 = 50%. Some other frequencies that are good to remember are:
- 1/3 Pot = 25%
- 1/2 Pot = 33%
- 2/3 Pot = 40%
- 3/4 Pot = 42%
- 4/5 Pot = 44%
- 1.5x Pot = 60%
- 2x Pot = 66%
- 3x Pot = 75%.
It’s rumored that a certain player named Isildur1 has used the latter numbers to his complete advantage! What if you thought about that first? You’d be probably playing the higher stakes. So now, having showed you how cool this math stuff is, let me show you how to apply it.
Pre-flop actions
First of all, let’s get into notice some flop hitting probabilities:
- A pair – 29%
- Two Pairs – 2%
- A Set (when holding a pocket pair) – 12%
- Trips – 1.35%
- A Full house – 0.09%
- Four of a Kind – 0.01%
- A pair or better - 32%
- A flush holding 2 suited cards – 0.84%
- A flush draw holding 2 suited cards – 11%
- A straight with suited non-gapped connectors – 1.31%
- An open-ended straight draw with non-gapped – 10.5%
- A straight with one-gapers – 0.98%
- An OESD with one-gapers – 8.08%
- A straight with two-gapers – 0.65%
- An OESD with two-gapers – 5.2%
- A gutshot (suited connectors) – 16.6%
- Any unsuited hand flopping 2p+ - 3.45%
- Any suited hand flopping 2p+/flush – 4.29%
- Suited connectors flopping 2p+/straight/flush – 5.59%
Having known all these, we are now inclined to play a more calculated game pre-flop. Although the reason for calling a raise pre-flop should not be pure mathematical, sometimes it does help to know how often you’ll flop an OESD + FD + pair or better with suited connectors, which is close to 50%.
I don’t like playing small suited connectors in multi-way pots, because usually you get dominated by higher flushes and you get the dummy end of a straight. They also aren’t that great to 3-bet against a raiser because they don’t have blockers, so what are we supposed to do with them when we’re not stealing blinds?
Well, let’s say that the EP raiser is opening a wide array of hands, like 14% and there’s also a caller, so we’re thinking with 56s in the BTN. This is a perfect spot to do the squeeze play, because 1) you’re getting a massive amount of folds, and 2) When you get called you will flop a lot of strong draws that you can represent along with your pairs and 2p+.
Poker can be a fun card game for the family, or a serious competitive game in which the steaks can be so enormous, even selling your house wouldn’t cover the costs.
There are many variations of poker, with Texas Hold ‘Em being the most popular worldwide.

Below are a whole bunch of poker facts and statistics which help you understand the chances of wining and the odds of getting the cards you want.
Did You Know?
A pocket pair is cards of the same rank, which means if your two cards have the same number, from 2-2 all the way up to A-A, this is called a pocket pair.
- The odds of receiving any pocket pair is 5.9% which is 16 to 1. These are also the same odds of receiving a pocket pair of 2’s.
- The odds of receiving a specific pocket pair: 0.45% or 220 to 1 These are the same odds for receiving a pocket pair of A’s.
- The odds of receiving a pocket pair of A’s twice in a row is 0.002047% or 48,840 to 1.
- The odds of receiving a pocket pair of K’s is 0.9% which is 220 to 1.
- The odds of receiving a pocket pair of Q’s is 1.4% which is 73 to 1.
- The odds of receiving a pocket pair of J’s is 1.8% which is 54 to 1.
- The odds of receiving a pocket pair of 10’s is 2.3% which is 43 to 1.
- The odds of receiving a pocket pair of 9’s is 2.7% which is 36 to 1.
- The odds of receiving a pocket pair of 8’s is 3.2 which is 31 to 1.
- The odds of receiving a pocket pair of 7’s is 3.6% which is 27 to 1.
- The odds of receiving a pocket pair of 6’s is 4.1% which is 24 to 1.
- The odds of receiving a pocket pair of 5’s is 4.5% which is 21 to 1.
- The odds of receiving a pocket pair of 4’s is 5.0% which is 19 to 1.
- The odds of receiving a pocket pair of 3’s is 5.4% which is 17 to 1.
Poker Fast Facts
The total number of possible royal flush hands in a standard 52 card deck is 4.
And the odds of making a royal flush is 649,739 to 1.
This is correct assuming that every game plays to the river.
In poker terms, the river is the name for the fifth card dealt, face-up on the board.
In total, there are 2,598,960 possible poker hands with 52 cards.
The odds of getting four of a kind in Texas Hold ‘Em is 4164 to 1.
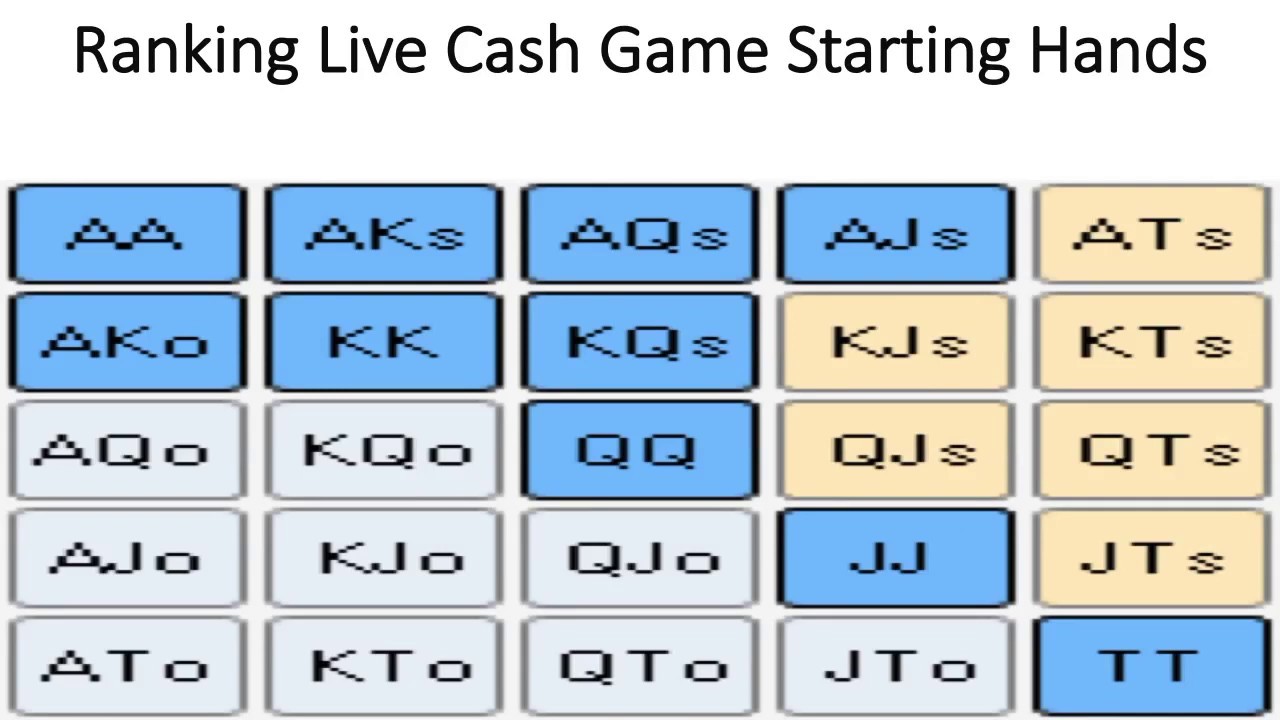
Basic Poker Statistics Games
Casinos normally change decks after 15 minutes of steady play, so that the cards can always be fresh and unmarked, as many professional players would be able to remember the certain markings on cards and use that to their advantage.
This is only a basic overview of poker odds, there are many calculators online that can help solve the odds of getting certain hands, depending on what stage of the game you’re at, what cards you currently hold and how many people are playing.
Basic Poker Statistics For Dummies
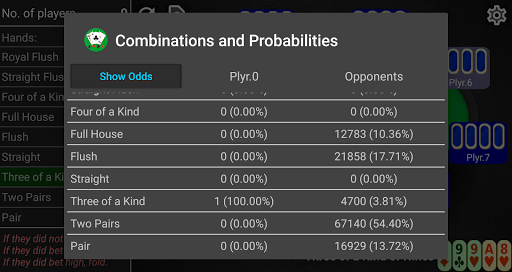
Basic Poker Statistics Cheat
Now you are familiar with these odds, you can use them to your advantage for a better poker strategy when you finally decided to play a tournament.
In Texas Hold-Em Poker the odds of making a royal flush hand is only 649,739 to 1.

